Search, Insert, Delete
- 자료구조의 가장 중요한 연산들
Array : 메모리의 연속된 공간
How to Store Items in an Array?
- Packed vs. Unpacked
: 배열이 항상 가득 찬 것은 아님
: 빈 자리를 한 쪽으로 모은다
- Sorted vs. Unsorted
: Item들이 정렬된 상태를 유지하느냐 아니냐
Packed, UnSorted : 아마도 가장 간단한 방법

Packed, UnSorted 성능
: Search : O(n) // 전부 다 보는 수밖에 없다 되게느리다.
: Insert : [Search, O(n)], O(1) // Worst Case를 따진다 -> Search해야되기 떄문에 느리다(작업자체는 빠름)
: Delete : [Search, O(n)], O(1) // Sorting이 안되어있으니까 뒤에서 들고오면 된다.
-> Insert와 Delete는 보통 Search를 먼저 수행함.

Pack, Sorted-> 제일 성능이 나오는 케이스

: Binary Search가 가능해진다.
packing이 되어서 저장이 되어 있는데 Sorting만 되어있으니까. Search가 달라진다.
: Item의 개수를 표시하는 변수가 따로 필요

근데 Insert, Delete는 packing이 되어 있고, insert할려니까 binary search를 사용하니까 사이에 들어가야 한다.
실패로 끝날때 index를 보면 사이에 들어가야한다는 것이 나온다.
Search가 빠른 대신, Insert, Delete가 느리다. 모두를 좋게 하는 방법은 없다. Search가 자주 일어나는 경우 좋음.
Unpacked, UnSorted
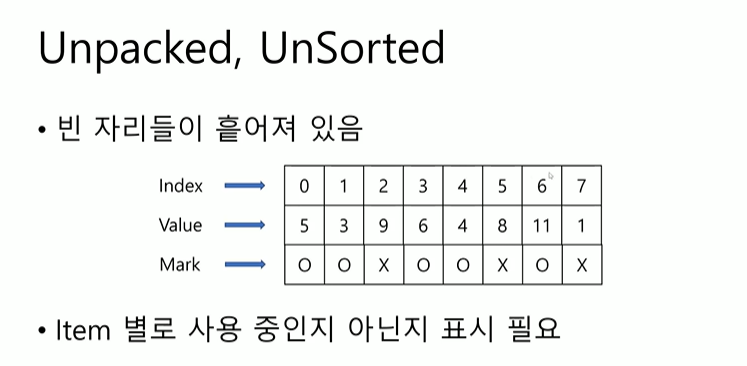
이전에는 빈자리들이 몰려있기 때문에 몇 개다 라는것만 표현하면 어디까지 쓰고, 어디까지 안쓰는지 알 수 있었는데, 다 흩어져 있기 때문에 쓴다 표시 필요하다. 변수 여러개를 한 단위로 생각하자.

Insert : 값을 넣는데 앞에서부터 쭉 찾으면서 안쓰는 칸 찾아서 저장하고 쓴다고 표시하면 된다. -> O(n)인거 같은데 기술을 추가하면 O(1)으로 줄일 수 있다. Unpacked, UnSorted 별로 좋은게 없다.
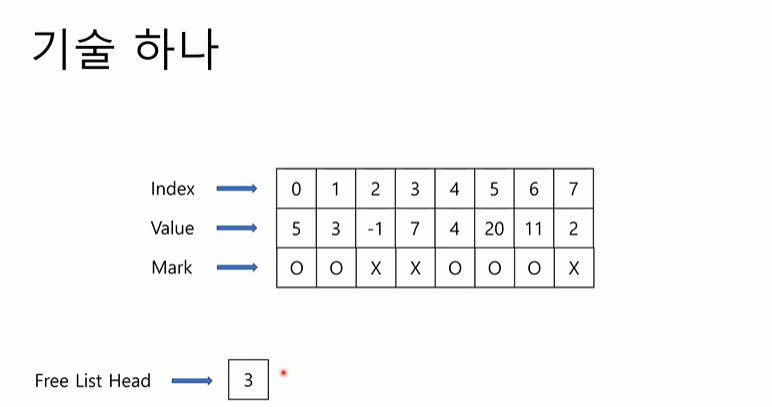
기술은 안쓴는칸은 빈자린데 의미없는 값을 Value에 넣어둔다. 3을 넣어주려고 한다. 3번 index라 하고 7번도 안쓴다.
3에서 index 3번 안쓰고 7번 안쓰고 거기서 또 가면 2번도 안쓰고 그 다음은 value -1이라서 끝난다. 이게 없으면 죽 훑으면서 빈자리를 찾아야 하는데 3번 안쓴다는걸 바로 알 수 있고, 7을 insert할 때 3을 지우고 7로 바꾼다.
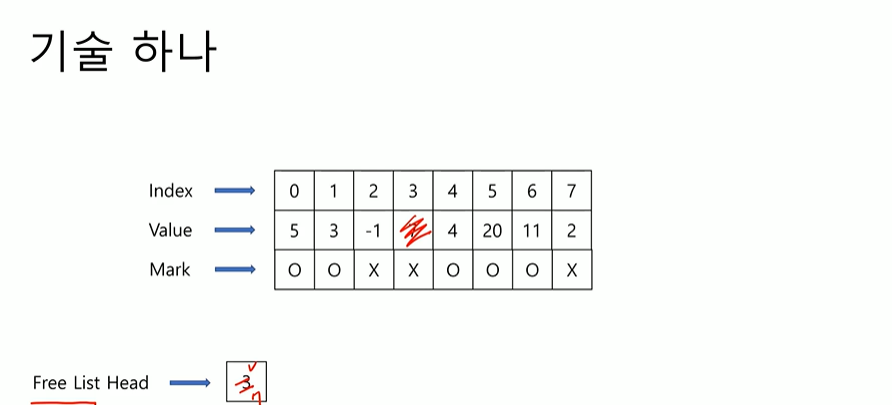
거기 있던 7을 가지고 온다. 여전히 7번통해서 2번까지 갈 수 있다. 이 기술을 쓰면 빈자리를 바로 찾을 수 있다. 그 다음에 delete 20을 한다라고 하면 20을 지워야 하는데 어떻게 지우냐. 5번 자리가 날라가는거니까 5번을 Free List Head로 가져오고, 안쓴다고 바꾼다. 20대신 3을 가져다 놓는다
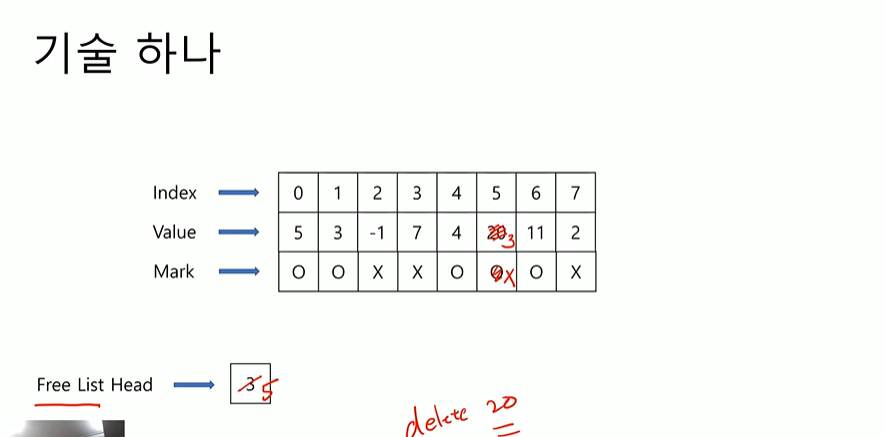
여전히 안쓰는 자리 전부 찾을 수 있고, 주어진 자리를 활용할 수 있다. 그래서 insert를 O(1)으로 할 수 있다. Search가 느린데 Insert, Delete는 빠르다. Byte수가 많으면 복사하는데 오래 걸린다.
실제로 디스크의 파일 폴더 디렉토리에 들어가면 파일 지우는 거 packed로 packing해서 유지하려면 뒤에서 갖다 옮겨야 되는데 안 쓴다고 마킹만 한다. 마킹만 하기때문에 delete는 빠르다. (현재는 모름)

Free List를 쓰는 다른 하드디스크.
Unpacked, Sorted

Sorting 해두는 부담을 갖는 것은, search가 빠르기 때문에 sorting하는 부담을 가지는데, binary search가 되나..?
쓰는 자리와 안쓰는 자리가 섞여있다. 중간을 찍었는데 안쓰는 자리이면..? -> 비교 불가.
기술 둘!
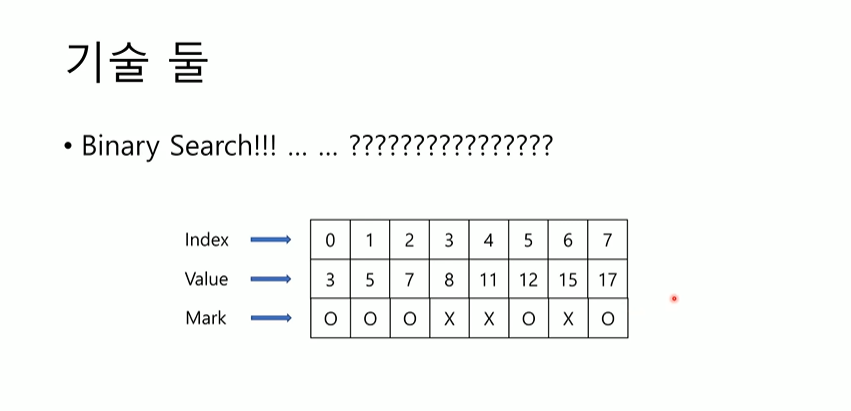
우선 처음에는 packed처럼 packing이 되어서 돌아간다. delete하기전에 처음에 insert할때는 중간에 빈자리를 두고 insert할 이유는 없다. Packed한것처럼 돌아간다. 첫 delete를 하기 전까지 중간에 빈자리가 안생긴다. delete를 하면 중간에 빈자리가 생기는데 중간에 있는 빈자리는 첫 delete를 할 때 생긴다. 그럼 이 자리는 delete된 자리라는 것을 알 수 있다. 변수가 하나더 필요하다. 사용한 제일 오른쪽 자리에 대한 자료가 필요하다. delete된 자리들은 거기 값을 그대로 나두는 것이다. 지워졌더라도 값은 그대로 살려둔다. 그러면 살아있는 값들과 죽어있는 값들을 다봤을때 sorting이 된걸로 유지를 할 수 있다. delete할때는 binary search로 하고 그냥 지워주면 아무것도 안바뀌니까 살아있는 값 죽어있는 값 다봐도 sorting이 되어 있다. 안쓴다고 marking만 하면 sorting 상태는 유지된다.

delete는 marking만 하면 되니까 O(1). Sorting된 order를 유지하기 위해서 예를 들어서 insert 16을 하려면 6,7사이에 들어가야한다고 나올텐데 약간 빠른 O(n)임. 예를 들어서 insert 4를 한다고 생각할 때, 빈자리까지만 밀면 된다.
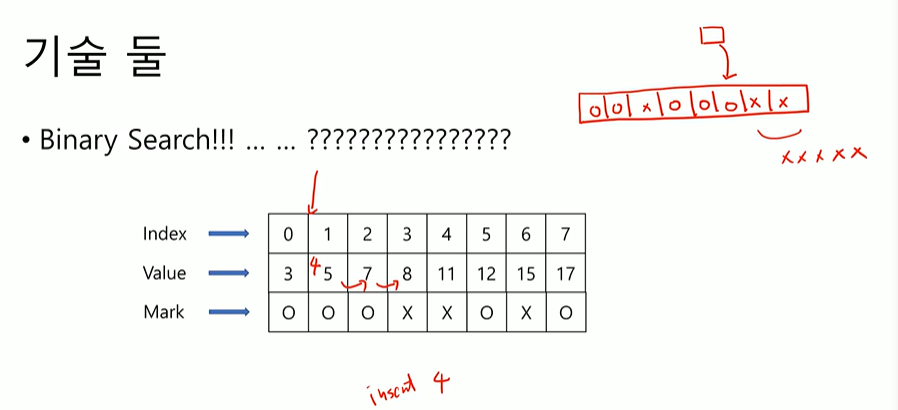
실제 내가 다루는 데이터가 어떤건지에 대해서 많은 영향을 받는다.